Source Code Java Newton-Raphson Method
>> 2.11.2012
Sekilas tentang Metode Newton-Raphson dari Wikipedia:
In numerical analysis, Newton's method (also known as the Newton–Raphson method), named after Isaac Newton and Joseph Raphson, is a method for finding successively better approximations to the roots (or zeroes) of a real-valued function. The algorithm is first in the class of Householder's methods, succeeded by Halley's method. The method can also be extended to complex functions and to systems of equations.
Untuk belajar tentang metode newton-raphson lebih dalam bisa di lihat disini http://numericalmethods.eng.usf.edu/topics/newton_raphson.html
Berikut ini kodingnya :
import java.util.*;
public class Newton{
public static Scanner sc = new Scanner(System.in);
public static double[] A;
public static double[] B;
public static double relApproxErrorLimit;
public static double Finitial(double x) {
double retVal = 0.0;
for (int i = A.length - 1; i >= 0; i--)
retVal += A[i] * Math.pow(x, i);
return retVal;
}
public static double Fder(double x) {
double retVal2 = 0.0;
for (int i = B.length - 1; i >= 0; i--)
retVal2 += B[i] * Math.pow(x, i);
return retVal2;
}
public static void printTableLine() {
for(int i = 0; i < 78; i++)
System.out.print('-');
System.out.println();
}
public static void findRoot(double Sval) {
double xnew =0.0;
double xold =0.0;
double prevApprox = 0.0;
int count = 0;
printTableLine();
System.out.printf("%10s %10s %10s %10s %10s \n", "Iterasi","x", "F(x)", "F'(x)", "% Galat");
printTableLine();
while (true) {
count++;
System.out.printf("%10d %10f %10f %10f ", count, Sval, Finitial(Sval),Fder(Sval));
xnew = Sval - Finitial(Sval) / Fder(Sval);
xold = Sval;
Sval = xnew;
System.out.printf("%10f \n", Math.abs((xnew - xold) / xnew * 100.0));
if (count > 1)
if (Math.abs((xnew - xold) / xnew * 100.0) < relApproxErrorLimit)
break;
if (count % 50 == 0) {
System.out.println();
System.out.println(" #" + count + " Iterasi Telah Dilakukan.");
System.out.println(" #Ketik 't' Untuk Menghentikan Iterasi.");
System.out.println(" #Ketik Selain 't' Untuk Melanjutkan Iterasi.");
System.out.println();
System.out.print("Lanjutkan? ");
String s = sc.next();
if (s.equals("T") || s.equals("t"))
break;
System.out.println();
}
}
printTableLine();
System.out.println();
System.out.println("\t Jumlah Iterasi : " + count);
System.out.println("\tBatas % Galat Relatif : " + relApproxErrorLimit);
System.out.println("\t Hampiran Akar : " + xnew);
System.out.println();
}
public static void main(String[] args) {
int N, M,O;
double Svalue;
while (true) {
System.out.print("Derajat Polinomial F(x) : ");
N = sc.nextInt();
System.out.println();
if (N >= 1)
break;
else {
System.out.println(" #Derajat Polinomial Harus > 0 !");
System.out.println();
}
}
System.out.println();
A = new double[N + 1];
for (int i = N; i >= 0; i--) {
System.out.print("Koefisien Derajat " + i + " : ");
A[i] = sc.nextDouble();
}
System.out.println();
while (true) {
System.out.print("Derajat Polinomial Turunan F(x) : ");
O = sc.nextInt();
System.out.println();
if (O >= 1)
break;
else {
System.out.println(" #Derajat Polinomial Harus > 0 !");
System.out.println();
}
}
System.out.println();
B = new double[O + 1];
for (int i = O; i >= 0; i--) {
System.out.print("Koefisien Derajat " + i + " : ");
B[i] = sc.nextDouble();
}
System.out.println();
while (true) {
System.out.print("Nilai awal (X0): ");
Svalue = sc.nextDouble();
System.out.println();
if (Svalue>0.0)
break;
else
{
System.out.println("Nilai awal harus lebih dari 0 !");
}
}
while (true) {
System.out.print("Digit Signifikan : ");
M = sc.nextInt();
System.out.println();
if (M >= 1)
break;
else {
System.out.println(" #Jumlah Digit Signifikan Harus > 0 !");
System.out.println();
}
}
relApproxErrorLimit = 0.5 * Math.pow(10, 2 - M);
System.out.println();
findRoot(Svalue);
}
}
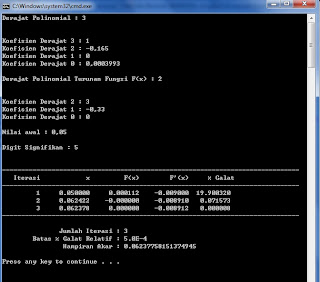
Screen Shot Program